Cyclic Quadrilaterals
Cyclic Quadrilaterals: Overview
This topic contains concepts like Cyclic Quadrilateral, Properties of Cyclic Quadrilateral, Cyclic Trapezium and Cyclic Parallelogram.
Important Questions on Cyclic Quadrilaterals
is a cyclic quadrilateral such that is a diameter of the circle. If and ,
is a cyclic quadrilateral where and , then find in degree .
Prove that any non-isosceles trapezium is not cyclic.
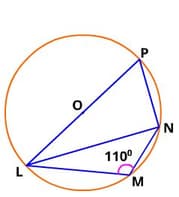
In the given figure, and are points on the semi-circle described on as diameter. Given that, angle and angle , then calculate angle
If the given figure, is the centre of the circle. The tangents at and intersect each other at point If is parallel to and find .
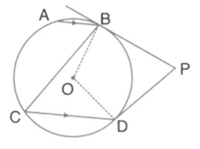
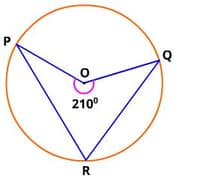
is a cyclic pentagon with centre of its circumcircle at point such that and angle . Calculate .
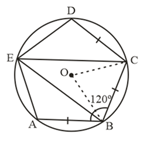
Consider the given figure.
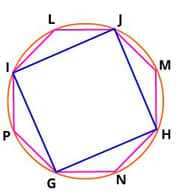
The measure of ∠ L + ∠ M + ∠ N + ∠ P = _____ degrees.
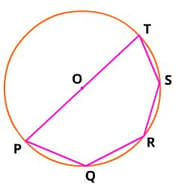
In the given figure, P, Q, R, S and T are points lying on the circumference of the circle. O is the centre and PT is the diameter of the circle.
The value of ∠ PQR + ∠RST = _____ degrees.
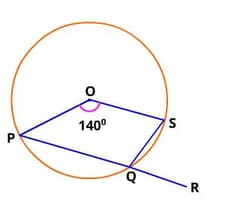
If O is the centre of the circle and side PQ is produced to R, then the measure of ∠ SQR = _____ degrees.
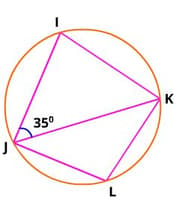
In the given figure, $ ∆$ IJK is an isosceles triangle with IJ = IK.
The measure of ∠ JLK = _____ degrees.
In the figure given, O is the centre of the circle and L, M, N and P are points on the circumference of the circle. LP is the diameter of the circle.
The measure of ∠ PLN = _____ degrees.
In the figure given, O is the centre of the circle and P, Q and R are points lying on the circumference of the circle.
The measure of ∠ PRQ = _____ degrees.
In the figure below points A, B, C and D lie on the circle and AD is its diameter. The measure of ∠BAC and ∠BCD is 30$ °$and$ 110°$.
The measure of ∠ADC is _____.
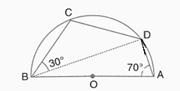
In the figure below, points and lie on the circle. The measures of and are and respectively.
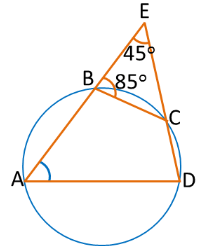
The measure of _____ degrees.
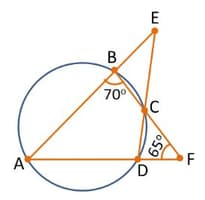
In the figure below, A, B, C and D are points on the circle. AB is extended to meet E and AD is extended to meet F.
The measure of ∠AED = _____ degrees.
Two circles intersect in point and . A secant passing through intersects the circles in and respectively. Tangents to the circles at and intersect at . Prove that and lie on a circle.
In the given figure, is tangent to the circle with centre , at point on its circumference and is parallel to Chord . If is a line segment , show that .
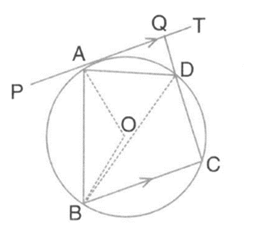
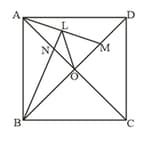
In a square , its diagonals and intersect each other at point . The bisector of angle meets at point and the bisector of angle meets at and at . show that :
is a cyclic quadrilateral.
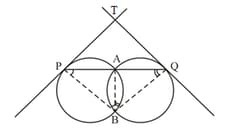
Two circles intersect each other at points and A straight line cuts the circles at and If the tangents at and intersect at point show that the points and are concyclic.
Prove that any four vertices of a regular pentagon are con-cyclic (lie on the same circle).